Pertidaksamaan Bilangan Real (Riil)

Sifat-Sifat Pertidaksamaan

1. Tanda pertidaksamaan tidak berubah jika kedua ruas ditambah atau dikurangi dengan bilangan yang sama

a < b maka:

a + c < b + c

a – c < b – c

2. Tanda pertidaksamaan tidak berubah jika kedua ruas dikali atau dibagi dengan bilangan positif yang sama

Jika a < b, dan c adalah bilangan positif, maka:

a.c < b.c

a/b < b/c

3. Tanda pertidaksamaan akan berubah jika kedua ruas pertidaksamaan dikali atau dibagi dengan bilangan negatif yang sama

Jika a < b, dan c adalah bilangan negatif, maka:

a.c > b.c

a/c > b/c

4. Tanda pertidaksamaan tidak berubah jika kedua ruas positif masing-masing dikuadratkan

Jika a < b; a dan b sama-sama positif, maka: a² < b²

Pertidaksamaan Linear

→ Variabelnya berpangkat 1

Penyelesaian:

Suku-suku yang mengandung variabel dikumpulkan di ruas kiri, dan konstanta diletakkan di ruas kanan

Contoh:

Pertidaksamaan Kuadrat

→ Variabelnya berpangkat 2

Penyelesaian:

1. Ruas kanan dibuat menjadi nol
2. Faktorkan
3. Tentukan harga nol, yaitu nilai variabel yang menyebabkan nilai faktor sama dengan nol
4. Gambar garis bilangannya

Jika tanda pertidaksamaan ≥ atau ≤, maka harga nol ditandai dengan titik hitam •

Jika tanda pertidaksamaan > atau <, maka harga nol ditandai dengan titik putih °

5. Tentukan tanda (+) atau (–) pada masing-masing interval di garis bilangan. Caranya adalah dengan memasukkan salah satu bilangan pada interval tersebut pada persamaan di ruas kiri.

Tanda pada garis bilangan berselang-seling, kecuali jika ada batas rangkap (harga nol yang muncul 2 kali atau sebanyak bilangan genap untuk pertidaksamaan tingkat tinggi), batas rangkap tidak merubah tanda

6. Tentukan himpunan penyelesaian

→ jika tanda pertidaksamaan > 0 berarti daerah pada garis bilangan yang diarsir adalah yang bertanda (+)

→ jika tanda  pertidaksamaan < 0 berarti daerah pada garis bilangan yang diarsir adalah yang bertanda (–)

Contoh:

(2x – 1)² ≥ (5x – 3).(x – 1) – 7

4x² – 4x + 1 ≥ 5x² – 5x – 3x + 3 – 7

4x² – 4x + 1 – 5x² + 5x + 3x – 3 + 7 ≥ 0

–x² + 4x + 5 ≥ 0

–(x² – 4x – 5) ≥ 0

–(x – 5).(x + 1) ≥ 0

Harga nol: x – 5 = 0 atau x + 1 = 0

x = 5 atau x = –1

Garis bilangan:

• menggunakan titik hitam karena tanda pertidaksamaan ≥
• jika dimasukkan x = 0 hasilnya positif
• karena 0 berada di antara –1 dan 5, maka daerah tersebut bernilai positif, di kiri dan kanannya bernilai negatif
• karena tanda pertidaksamaan ≥ 0, maka yang diarsir adalah yang positif

Jadi penyelesaiannya: {x | –1 ≤ x ≤ 5}

Pertidaksamaan Tingkat Tinggi

→ Variabel berpangkat lebih dari 2
Penyelesaian sama dengan pertidaksamaan kuadrat
Contoh:
(2x + 1)².(x² – 5x + 6) < 0
(2x + 1)².(x – 2).(x – 3) < 0
Harga nol: 2x + 1 = 0 atau x – 2 = 0 atau x – 3 = 0
x = –1/2 atau x = 2 atau x = 3
Garis bilangan:

• menggunakan titik putih karena tanda pertidaksamaan <
• jika dimasukkan x = 0 hasilnya positif
• karena 0 berada di antara –1/2 dan 2, maka daerah tersebut bernilai positif
• karena –1/2 adalah batas rangkap (–1/2 muncul sebanyak 2 kali sebagai harga nol, jadi –1/2 merupakan batas rangkap), maka di sebelah kiri –1/2 juga bernilai positif
• selain daerah yang dibatasi oleh batas rangkap, tanda positif dan negatif berselang-seling
• karena tanda pertidaksamaan ³ 0, maka yang diarsir adalah yang positif

Jadi penyelesaiannya: {x | 2 < x < 3}

Pertidaksamaan Pecahan

→ ada pembilang dan penyebut
Penyelesaian:

1. Ruas kanan dijadikan nol
2. Samakan penyebut di ruas kiri
3. Faktorkan pembilang dan penyebut (jika bisa)
4. Cari nilai-nilai variabel yang menyebabkan pembilang dan penyebutnya sama dengan nol (harga nol untuk pembilang dan penyebut)
5. Gambar garis bilangan yang memuat semua nilai yang didapatkan pada langkah 4

Apapun tanda pertidaksamaannya, harga nol untuk penyebut selalu digambar dengan titik putih (penyebut suatu pecahan tidak boleh sama dengan 0 agar pecahan tersebut mempunyai nilai)

6. Tentukan tanda (+) atau (–) pada masing-masing interval

Contoh 1:

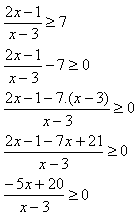
Harga nol pembilang: –5x + 20 = 0
–5x = –20 → x = 4
Harga nol penyebut: x – 3 = 0 → x = 3
Garis bilangan:
→ x = 3 digambar menggunakan titik putih karena merupakan harga nol untuk penyebut

Jadi penyelesaiannya: {x | 3 < x ≤ 4}

Contoh 2:

Harga nol pembilang: x – 2 = 0 atau x + 1 = 0
x = 2 atau x = –1
Harga nol penyebut: tidak ada, karena penyebut tidak dapat difaktorkan dan jika dihitung nilai diskriminannya:
D = b² – 4.a.c = 1² – 4.1.1 = 1 – 4 = –3
Nilai D-nya negatif, sehingga persamaan tersebut tidak mempunyai akar real
(Catatan: jika nilai D-nya tidak negatif, gunakan rumus abc untuk mendapat harga nol-nya)
Garis bilangan:

Jadi penyelesaiannya: {x | x ≤ –1 atau x ≥ 2}